Configuring the optimization model for the object-centric Material Allocation app
The stock transfers proposed by the Material Allocation app are achieved through constraint-based optimization. We now provide this capability using the Optimization Engine, which is a Celonis platform capability that is currently used by the Material Allocation app and the upcoming Load Consolidation app. The Optimization Engine is a frontend where you can create, populate, and solve Mixed Integer Linear Programming (MILP) models. You can change the optimization model for existing applications, and create net-new models for your own use cases, without involving a Celonis engineer.
The Optimization Engine is in Limited Availability status. It runs through a dedicated Machine Learning job which we need to enable before you can use it. Raise a Service Desk ticket or talk to your Celonis point of contact to get access.
You’ll need to grant the Machine Learning job the following permissions:
On the Studio package for your use case (for example, the Studio package for the business app), Use package and Edit package permissions.
In the data pool where you’re working with objects and events (the OCPM Data Pool or another if you have multiple data pools enabled), Use all data models, View data pool, Edit data pool, Data Push API, and Continuous Data Push API.
To configure your optimization model using Optimization Engine’s UI, go to the URL team_base_url/machine-learning/ui/optimization-engine, where team_base_url is the base URL for your Celonis team (for example https://example_team.example_cluster.celonis.cloud/). You can run the optimization model from the UI.
You can also choose to configure your optimization model using a JSON script instead of the user interface. You can schedule the script to run regularly. If you want to do this, let us know when you request access to the Optimization Engine, and we’ll send you the instructions.
The optimization model
When you configure an optimization model with the Optimization Engine, you’re creating a Mixed Integer Linear Programming (MILP) model. MILP models have three components:
Decision variables: An unknown quantity that is to be optimized. The calculated value must be a non-negative continuous real number, a non-negative integer, or binary (0 or 1). The optimization model can include many decision variables. Together the results describe the optimal solution to the problem expressed in the model.
Constraints: An inequality or equality (equation) that restricts the possible values one or more decision variables can have. The expression comprises a left side, a comparison operator, and a right side. Each side can contain one or many parameters, decision variables, or a combination of those. Examples of parameters are demand quantity, unit price, and shipping cost. The optimization model can include many constraints, and they can be reused across decision variables.
Objective function: A function that defines the result of the optimization. The objective function states whether it is aiming to maximize or minimize the result of the optimization for the decision variables, subject to the constraints. The objective function usually includes one or more of the decision variables, and zero, one, or multiple related parameters, such as the costs of transferring a material, or the revenue for each unit sold. The optimization model can include only one objective function.
Your optimization model can also contain constants, consisting of a name and integer value. You can use constants as part of constraints.
The data sources that provide input for the optimization model can be objects from a perspective, KPIs or calculated attributes from a Knowledge Model, or a combination of both.
You can use the existing object types in your object-centric data model and their attributes to help you decide on your decision variables and their dimensions.
You can create dedicated object types to be used only as decision variables, and add them to a perspective. Use the prefix DecisionVariable for the name of the object type if you’re doing that.
You can create standalone helper objects in a perspective (see Helper objects) to contain a specific input attribute that you don’t have as an attribute of an existing object type, such as a workday calendar.
If a calculation could be done either in your optimization model, or in a PQL expression in a KPI or calculated attribute, choose to do it in a PQL expression to reduce the computation time for your optimization model. For example, calculated attributes can contain business logic such as quantity conversion or currency conversion.
Optimization model example: Product mix for a bakery
In this example, we’ll look at an optimization model to suggest the optimal product mix for a bakery. It’s a Mixed Integer Linear Programming (MILP) model for maximizing the revenue generated by cakes sold, subject to available ingredient quantities.
Decision Variables
The quantity of each cake to bake for sale is described as xc, with each c being a different kind of cake (for example, red velvet cake, date and walnut cake, strawberry cake).
The value of the variable x is logically a non-negative integer, because it isn't possible to bake a negative amount of cake, or a fraction of a cake. We could also define the value as a continuous real number, and round up or down to the nearest complete cake. That approach would help improve the performance for a model with more complexity and more possible solutions.
Objective Function
We want to maximize the total revenue from selling cakes, which is the sum of the revenue from each type of cake times the number of cakes baked. Pc is the price at which a given cake can be sold. Here's the function:
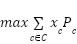
The price and quantity of baked cakes are multiplied and then summed up. In this example, both the price and the baked cakes are multiplicands, while the summation over all cakes is a summand.
Constraints
Each cake needs certain ingredients for its recipe. The availability of ingredients ultimately determines how many of a given cake can be made, as you can’t make a strawberry cake without strawberries, for example.
The ingredients ( flour, sugar, eggs, and so on) are denoted as i. The constraint needs to be created for every ingredient i. The currently available quantity of an ingredient i is denoted as Qi. The recipe quantity which each cake needs of a given ingredient is given as Rci. For example, a coffee cake requires 300 grams of flour. Here’s the constraint:
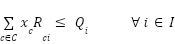
In this example, the quantities of baked cakes, recipe, and available ingredients are each multiplicands. The recipe and quantities of baked cakes are summed up over all cakes and held on the left hand side of the inequality, while the available quantity is held on the right hand side of the inequality. The available quantity is still wrapped in a summand, but there is no summation happening since the only index (the ingredient) is already an iteration index for the constraint. Essentially, we add up the quantity of flour (for example) used to bake all cakes while ensuring we do not consume more flour than currently available.